14(2)

下部分的体积为 VB−AEFD,VB−CDFGV_{B-AEFD},V_{B-CDFG} 两个四棱锥的体积之和，直接算出来，上面的体积是总体积减去下面的体积。

15(4)

设数列极限为 LL，an+1=an+an−1  ⟺  an+1an=1+an−1an  ⟹  L=1+1La_{n+1}=a_n+a_{n-1}\iff \frac{a_{n+1}}{a_n}=1+\frac{a_{n-1}}{a_n}\implies L=1+\frac{1}{L}，由于 L>0L>0，解得 L=1+52L=\frac{1+\sqrt 5}{2}。

17

看错字母，只剩 3 分。

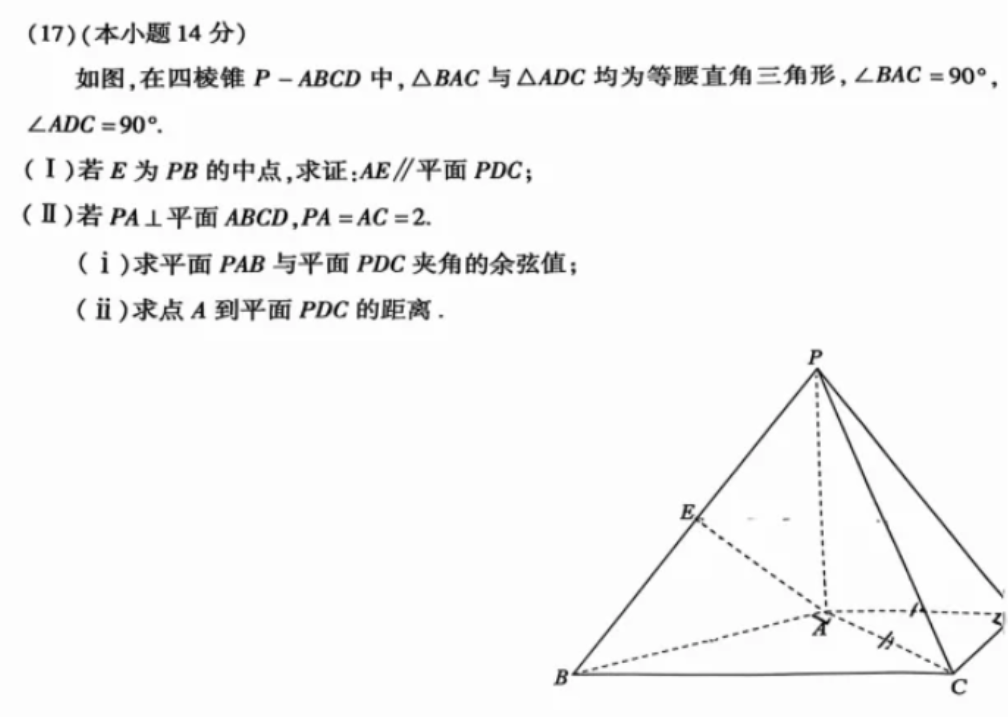
(1)

作 CPCP 中点 FF，连接 EF,DFEF,DF。
∵E,F\because E,F 为 BP,CPBP,CP 中点
∴EF∥BC,EF=12BC\therefore EF \parallel BC,EF=\frac{1}{2} BC
∵ΔADC\because \Delta ADC 为等腰直角三角形
∴AC=2AD,∠ACD=45°\therefore AC=\sqrt 2 AD,\angle ACD=45°
∵ΔABC\because \Delta ABC 为等腰直角三角形
∴BC=2AC=2AD,∠ACB=45°\therefore BC=\sqrt 2 AC=2AD,\angle ACB=45°
∴AD∥BC,AD=12BC\therefore AD\parallel BC,AD=\frac{1}{2}BC
∴AD∥EF,AD=EF\therefore AD\parallel EF,AD=EF
∴\therefore 平行四边形 ADFEADFE
∴AE∥DF\therefore AE\parallel DF
∵DF⊂\because DF \subset 平面 PDCPDC，AE⊄AE \not\subset 平面 PDCPDC
∴AE∥\therefore AE\parallel 平面 PDCPDC

(2)

∵PA⊥\because PA\perp 平面 ABCDABCD，AB⊂AB\subset 平面 ABCDABCD，AC⊂AC\subset 平面 ABCDABCD，∠BAC=90°\angle BAC=90°
∴PA⊥AB,PA⊥AC,AB⊥AC\therefore PA\perp AB,PA\perp AC,AB\perp AC
以点 AA 为原点，AB,AC,APAB,AC,AP 所在直线为 x,y,zx,y,z 轴，建立空间直角坐标系，
A(0,0,0),B(2,0,0),C(0,2,0),D(−1,1,0),P(0,0,2)A(0,0,0), B(2,0,0), C(0,2,0), D(-1,1,0), P(0,0,2)
∵AB→=(2,0,0),AP→=(0,0,2)\because \overrightarrow{AB}=(2,0,0),\overrightarrow{AP}=(0,0,2)
设平面 PABPAB 的法向量 m⃗=(x1,y1,z1)\vec m=(x_1,y_1,z_1)，
{m⃗⋅AB→=0m⃗⋅AP→=0  ⟹  {2x1=02z1=0\small \begin{cases} \vec m \cdot \overrightarrow{AB}=0 \\ \vec m\cdot \overrightarrow{AP}=0 \end{cases}\implies \small \begin{cases} 2_{x_1}=0 \\ 2_{z_1}=0 \end{cases}
令 y1=0y_1=0，则 m⃗=(0,1,0)\vec m=(0,1,0)。
∵PC→=(0,2,−2),PD→=(−1,1,−2)\because \overrightarrow{PC}=(0,2,-2),\overrightarrow{PD}=(-1,1,-2)
设平面 PCDPCD 的法向量 n⃗=(x2,y2,z2)\vec n=(x_2,y_2,z_2)，
{n⃗⋅PC→=0n⃗⋅PD→=0  ⟹  {2y2−2z2=0−x2+y2−2z2=0\small \begin{cases} \vec n \cdot \overrightarrow{PC}=0 \\ \vec n\cdot \overrightarrow{PD}=0 \end{cases}\implies \small \begin{cases} 2{y_2}-2_{z_2}=0 \\ -{x_2}+y_2-2{z_2}=0 \end{cases}
令 y2=1y_2=1，则 n⃗=(−1,1,1)\vec n=(-1,1,1)。
设平面 PAB,PCDPAB,PCD 夹角为 θ\theta，则
cos⁡θ=∣n⃗⋅m⃗∣n⃗∣∣m⃗∣∣=33\cos \theta=|\frac{\vec n\cdot \vec m}{|\vec n||\vec m|}|=\frac{\sqrt 3}{3}

3

AC→=(0,2,0)\overrightarrow{AC}=(0,2,0)
设点 AA 到平面 PDCPDC 的距离为 dd，
则 d=AC→⋅n⃗∣n⃗∣=233d=\overrightarrow{AC}\cdot \frac{\vec n}{|\vec n|}=\frac{2\sqrt 3}{3}

18(2)

三角形面积公式代错边，只剩 3 分。


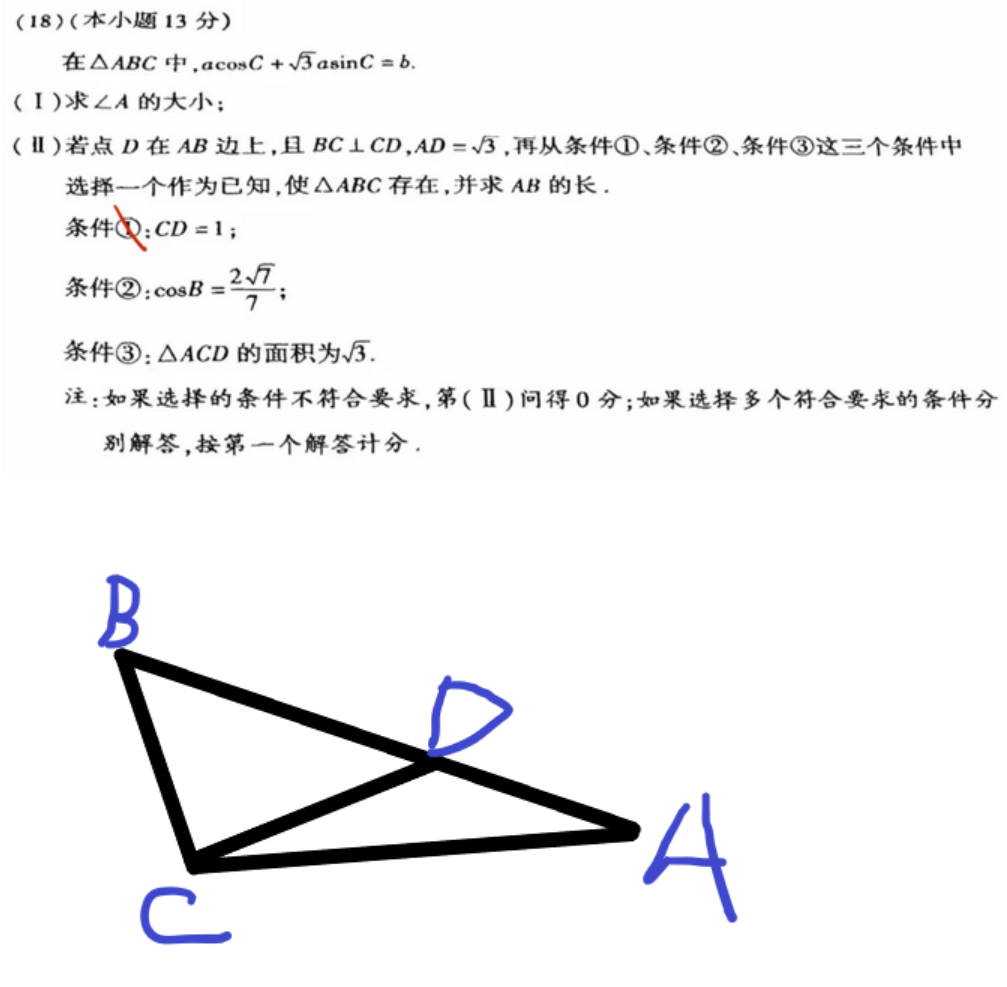
选 3。

∵SΔACD=3\because S_{\Delta ACD}=\sqrt 3
∴12AD⋅ACsin⁡A=3,AC=4\therefore\frac{1}{2} AD\cdot AC \sin A=\sqrt 3,AC=4
∵CD2=AC2+AD2−2AD⋅ACcos⁡A\because CD^2=AC^2+AD^2-2AD\cdot AC\cos A
∴CD=7\therefore CD=\sqrt 7
∵sin⁡∠ADCAC=sin⁡∠ACD,π2<∠ADC<π\because \frac{\sin \angle ADC}{AC}=\frac{\sin \angle A}{CD},\frac{\pi}{2}<\angle ADC< \pi
∴sin⁡∠ADC=277\therefore \sin \angle ADC=\frac{2\sqrt{7}}{7}
∴cos⁡∠CDE=−cos⁡∠ADC=1−sin⁡2∠ADC=217\therefore \cos \angle CDE=-\cos \angle ADC=\sqrt{1-\sin^2 \angle ADC}=\frac{\sqrt{21}}{7}
∵BC⊥CD\because BC\perp CD
∴∠BCD=π2,RtΔBCD\therefore\angle BCD=\frac{\pi}{2},Rt\Delta BCD 中 BD=CDcos⁡∠CDE=733BD=\frac{CD}{\cos \angle CDE}=\frac{7\sqrt 3}{3}
∴AB=BD+AD=1033\therefore AB=BD+AD=\frac{10\sqrt 3}{3}

19(2)

没有讨论 1a=2\frac{1}{a}=2。

20

(1)

算错数了。

(2)

求二阶导，分子是 (4−2π+2cos⁡x)sin⁡x(4-2\pi+2\cos x)\sin x，放缩成比 (6−2πsin⁡x)<0(6-2\pi \sin x)<0 小，所以 g′(x)g'(x) 在 (0,π2)(0,\frac{\pi}{2}) 上单调递减，找点即可。

(3)

21(3)

01 教的做法！

设数字 xx 在 QQ 的元素中出现的次数为 cxc_x，有 ∑cx=4n\sum c_x=4n。
∵\because 性质 22
∴∑(cx2)=∑i<jAi∩Aj=(n2)  ⟹  ∑cx(cx−1)=∑cx2−∑cx=∑cx2−4n=n(n−1)  ⟹  ∑cx2=n2+3n\therefore \sum \binom{c_x}{2}=\sum\limits_{i<j} A_i\cap A_j=\binom{n}{2}\implies \sum{c_x(c_x-1)}=\sum{c_x^2}-\sum c_x=\sum{c_x^2}-4n=n(n-1)\implies \sum{c_x^2=n^2+3n}
与 (2) 同理可证 ∀x,cx≤4\forall x,c_x\leq 4。因此 ∑cx2≤4∑cx  ⟺  n2+3n≤16n\sum{c_x^2}\leq 4\sum c_x\iff n^2+3n\leq 16n，解得 n≤13n\leq 13，在 ∀x,cx=4\forall x,c_x=4 时取等。可以给出一个合法的构造使得 n=13n=13（但是证明为什么可以给出一组构造是困难的），因此 nmax⁡=13n_{\max}=13。